Detail from John Martin's "The Bard"
Walking the Dog
Henry Holiday alluding to John Martin
Doré (1863), Holiday (1876), Doré (1866)
Holiday and Gheeraerts I
Holiday - Millais- Anonymous - Galle, detail
An Expedition Team
The Hunting of the Snark
Ipernity's Dragon
Rabenschwarz
Crows are Artists too!
h91
h90
h80
h70
h60
h50
h40
h30
h20
h12
h11
h10
Beagle Laid Ashore
Beagle Laid Ashore (2)
Beagle Landing
Hans Holbein, The Ambassadors, 1533 (modified)
pictorial allusions
A Nose Job
Bremsklötze niederwalzen!
Trumpet
MeQR
Me
Neuman, Butcher, Jowett
Anne Hale Mrs. Hoskins
Ikegami matsuri
Taichung Temple
A new Antenna
"Shinjuku Business Hotel" at Night
Cat
SnarkLogo
SnarkLogo r
See also...
Keywords
Authorizations, license
-
Visible by: Everyone -
All rights reserved
-
1 193 visits
Optimum Inequaliy
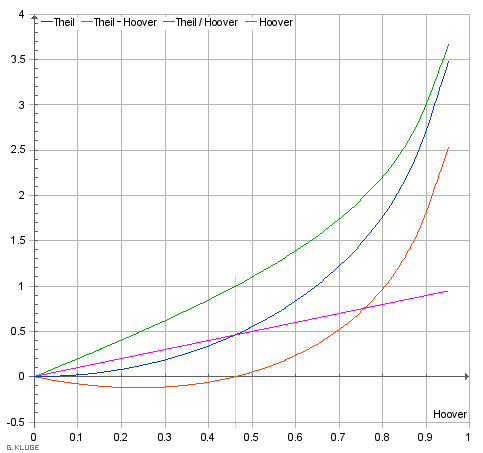

Assumption: There is a degree of inequality of resource distribution which leads to a minimum of redistribution conflicts. We find that range between a Hoover inequality of 0.2 and 0.3. Scandinavian societies get closest to that.
You know the 80/20 rule. This is similar to a way to describe inequal resource distributions: E.g. "80/20" could describe a situation where 80% of people own 20% of all resources, and 20% of people own 80% of ressources. (For distributions described in this way, the Hoover inequality is equal to the Gini inequality.)
From this you can compute another inequality measure: the Hoover inequality:
100/0 -> 1
90/10 -> 0.8
80/20 -> 0.6
70/30 -> 0.4
60/40 -> 0.2
50/50 -> 0
Yet another inequality is the symmetric Theil redundancy:
100/0 -> indefinitely large
90/10 -> 1.758
80/20 -> 0.832
70/30 -> 0.339
60/40 -> 0.081
50/50 -> 0
Formulas for the Theil-S redundancy and the Hoover inequality: www.poorcity.richcity.org
=== Meaning ===
The symmetric Theil redundancy (blue curve) applies to redistribution processes which are perfectly stochastic. Example: Equalization processes in ideal gases.
The Hoover inequality (purple curve) applies to intelligent redistribution of inequal distributions with minimum effort based on perfect knowledge about the distribution at any time. (For the groups split into one wealthy and one less wealthy part, the Hoover inequality is similar to the better known Gini inequality.)
The difference (red curve) between both is information. (You see that once you look at the formulas.)
On the left side the difference is negative. Societies in this range usually accept some inequality. Do people perceive an "information" which makes them want to reduce the inequality?
On the right side the difference is positive. In societies in this range there usually are more complaints about inequality. Do people perceive an "information" which lets them tolerate a certain inequality? (Inequalities with the most negative differences can be found e.g. in Scandinavian countries.)
Is that so? Can we compute and predict the acceptability of inequal resource distribunions?
I am an engieer, not an economist. But we all know that there are tolerable inequalities and extreme inequalities which lead to violent redistribution processes.
You know the 80/20 rule. This is similar to a way to describe inequal resource distributions: E.g. "80/20" could describe a situation where 80% of people own 20% of all resources, and 20% of people own 80% of ressources. (For distributions described in this way, the Hoover inequality is equal to the Gini inequality.)
From this you can compute another inequality measure: the Hoover inequality:
100/0 -> 1
90/10 -> 0.8
80/20 -> 0.6
70/30 -> 0.4
60/40 -> 0.2
50/50 -> 0
Yet another inequality is the symmetric Theil redundancy:
100/0 -> indefinitely large
90/10 -> 1.758
80/20 -> 0.832
70/30 -> 0.339
60/40 -> 0.081
50/50 -> 0
Formulas for the Theil-S redundancy and the Hoover inequality: www.poorcity.richcity.org
=== Meaning ===
The symmetric Theil redundancy (blue curve) applies to redistribution processes which are perfectly stochastic. Example: Equalization processes in ideal gases.
The Hoover inequality (purple curve) applies to intelligent redistribution of inequal distributions with minimum effort based on perfect knowledge about the distribution at any time. (For the groups split into one wealthy and one less wealthy part, the Hoover inequality is similar to the better known Gini inequality.)
The difference (red curve) between both is information. (You see that once you look at the formulas.)
On the left side the difference is negative. Societies in this range usually accept some inequality. Do people perceive an "information" which makes them want to reduce the inequality?
On the right side the difference is positive. In societies in this range there usually are more complaints about inequality. Do people perceive an "information" which lets them tolerate a certain inequality? (Inequalities with the most negative differences can be found e.g. in Scandinavian countries.)
Is that so? Can we compute and predict the acceptability of inequal resource distribunions?
I am an engieer, not an economist. But we all know that there are tolerable inequalities and extreme inequalities which lead to violent redistribution processes.
- Keyboard shortcuts:
Jump to top
RSS feed- Latest comments - Subscribe to the comment feeds of this photo
- ipernity © 2007-2024
- Help & Contact
|
Club news
|
About ipernity
|
History |
ipernity Club & Prices |
Guide of good conduct
Donate | Group guidelines | Privacy policy | Terms of use | Statutes | In memoria -
Facebook
Twitter
¤ Yoram Amiel: Thinking about Inequality: Personal Judgment and Income Distributions, 2000
¤ Amartya Sen: On Economic Inequality, 1973 (Enlarged Edition with a substantial annexe after a Quarter Century with James Foster, Oxford 1997)